Home page

Il calcolo della marea astronomica

Il calcolo della marea può essere eseguito con relativa facilità da chi conosce le basi di un qualunque linguaggio di programmazione. Con un po' più di lavoro il calcolo può essere effettuato anche con l'ausilio di una normale calcolatrice scientifica.

Per un dato istante l'altezza di marea è data dalla somma delle altezze A di una serie di onde elementari, indicate come componenti di marea.
La figura sotto riportata mostra, a titolo di esempio, due componenti di diverso periodo, altezza e fase, e la loro risultante.

Ogni componente è esprimibile con l'equazione: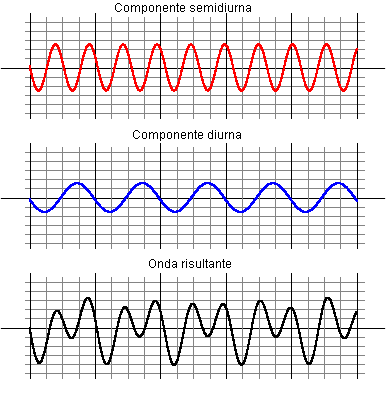

A = f H cos(alfa°)

H è la semiampiezza media dell'onda in cm ed è una caratteristica costante del luogo
f è un fattore correttivo della semiampiezza e dipende dalla posizione della Luna. E' fornito da apposite tabelle.
alfa° è l'angolo complessivo di fase dell'onda reale all'istante considerato

Alfa° è costituito da tre parti:

alfa° = (V_o+u)+Omega*t-g°

(V_o+u) è l'angolo di fase iniziale e corrispondente all'istante t_o dal quale si parte per calcolare la marea. Normalmente, si assume come istante iniziale t_o le ore locali 00.00 del 1.o Gennaio dell'anno. E' fornito da apposite tabelle (vedi oltre).
Omega è la velocità angolare oraria dell'onda; è un elemento praticamente costante ed è noto.
Omega*t è l'incremento di fase accumulato a partire dall'istante iniziale t_o sino all'istante per il quale si effettua il calcolo.
t è il tempo trascorso a partire dall'istante iniziale espresso in ore (ad es. per le ore 15 del 10 Marzo t=1647 h)
g° è l'angolo di ritardo della fase; ritardo con il quale l'onda di marea reale si presenta sul luogo rispetto all'onda teorica. Esso è dovuto all'inerzia della massa liquida e agli attriti e resistenze che incontra la massa d'acqua nello spostarsi. E' una caratteristica costante del luogo.

H e g° sono denominate costanti armoniche per ciascuna onda e sono i due elementi che, in una data località, la caratterizzano.
Noti dunque questi due valori per ogni componente è possibile calcolare la marea.
La formula iniziale assume dunque la forma più universalmente nota:

A = f H cos((V_o+u)+Omega*t-g°)

Le costituenti armoniche
Il numero delle costituenti armoniche da utilizzare dipende dalla località. In genere è sufficiente un numero compreso tra sette a dieci per avere una precisione dell'ordine del centimetro, ma talvolta se ne devono utilizzare anche molte di più. Ad ogni componente è associata la posizione di un astro fittizio che esprime un comportamento particolare della Luna o del Sole.
Ogni componente ha una propria velocità angolare oraria universalmente valida, mentre, per una data località, è caratterizzata dalle sue costanti armoniche H e g°.
A seconda del periodo, rispetto al giorno solare, le componenti si definiscono diurne e semidiurne. Sono diurne quelle che in 24 ore solari presentano un massimo ed un minimo, semidiurne quelle che presentano due massimi e due minimi.
Le principali componenti del Mar Mediterraneo sono

Componente	Tipo	Velocità °/h
M2	semidiurno	28.9841°/h
S2	semidiurno	30°/h
N2	semidiurno	28.43973°/h
K2	semidiurno	30.08214°/h
K1	diurno	15.04107°/h
O1	diurno	13.94306°/h
P1	diurno	14.95893°/h
S1	diurno	15°/h
M4	quadridiurno	57.97°/h
MS4	quadridiurno	58.98°/h

I fattori nodali
I valori f ed u presenti nelle formule sono detti fattori nodali in quanto dipendono dalla posizione dei nodi dell'orbita lunare e sono fattori correttivi, il primo della altezza dell'onda ed il secondo dell'angolo di posizione iniziale. La loro variabilità segue un ciclo di circa 18 anni.
I valori sono tabellati con ampio anticipo di anni e quindi sono facimente reperibili; le tabelle forniscono f ed u generalmente per la metà dell'anno, mentre la parte principale V_o è calcolata per il 1.o di Gennaio.
L'elemento (V_o+u) è pertanto un ibrido costituito da due parti calcolate per periodi diversi ma complessivamente e convenzionalmente riferito al 1.o Gennaio.
I due fattori f ed u variano molto lentamente e, nel calcolo pratico, vengono considerati costanti per tutto l'anno anche se a rigore non lo sono. Questa approssimazione non comporta errori significativi nel calcolo dell'altezza ed ha il vantaggio di non richiedere il calcolo di f ed u, che è abbastanza gravoso, per l'istante effettivo.
I fattori nodali sono diversi per ogni componente ma validi per qualunque località del mondo.
Sotto è fornita una applicazione interattiva in Javascript che fornisce f e (V_o+u) per qualunque anno impostato.

Calcolatore Fattori Nodali
Anno:
Componente	f	(Vo+u)°
M2
S2
N2
K2
K1
O1
P1
S1
M4
MS4

Il fattore "f" e la parte variabile "u" di (Vo+u) sono calcolati, secondo la consuetudine,
per il 1.o Luglio, mentre la parte principale "Vo" di (Vo+u) è calcolata per il 1.o Gennaio.

Il ritardo di fase
A volte in luogo del ritardo di fase g°, viene fornito il valore k°.
Il valore g° è niente altro che k° al quale sono state apportate alcune correzioni per poter utilizzare la variabile tempo t riferendola direttamente al fuso della località anzichè al meridiano di Greenwich.
Noto k°, g° si ottiene con la seguente espressione:

g° = k - pL + Lf * omega

pl è il prodotto della longitudine in gradi del luogo per il pedice del nome dell'onda (es. 1 per K1, 2 per M2)
Lf è la longitudine in ore del fuso al quale appartiene la località ( in Italia è +1 per l'ora invernale e +2 per l'ora estiva)
omega è la già nota velocità oraria dell'onda.

Il calcolo pratico
Per effettuare il calcolo dell'altezza di marea per una data ora locale occorre dunque, per ogni componente

• Reperire le due costanti armoniche H e g° (se è dato solo k° trasformarlo in g°)
• Reperire l'altezza del livello medio del mare Z₀ (che è identica per tutte le componenti)
• Determinare i fattori nodali f e (V_o+u) per l'anno in corso
• Per l'ora locale considerata determinare le ore t trascorse a partire dalle ore 00.00 del 1o Gennaio
• Moltiplicare la velocità angolare oraria omega per il tempo trascorso t
• Sommare (V_o+u), il prodotto omega*t e l'angolo g°
• Calcolare il coseno dell'angolo di fase complessivo
• Moltiplicare per f e per H

Alla somma delle altezze così calcolate va aggiunto il livello medio del mare Z_o per avere l'altezza di marea all'istante voluto.
Il calcolo può essere estrapolato anche oltre l'anno considerato, in particolare se non si dispone dei fattori nodali. Ciò comporterà inevitabilmente alcune piccole imprecisioni, ma l'andamento generale dell'onda di marea non sarà molto dissimile da quello corretto.

Esempio Applichiamo quanto sopra ad un caso reale.
Sul sito del comune di Venezia sono fornite le costanti armoniche H e k° ed il livello medio del mare.

Componente	H	k°	pL	Lf*om	corr.	g°
M2	24.8	308°	-24.68°	28.98°	4.3°	312.3°
S2	14.5	318°	-24.68°	30°	5.3°	323.3°
N2	4.1	307°	-24.68°	28.44°	3.8°	310.8°
K2	4.3	311°	-24.68°	30.08°	5.4°	316.4°
K1	17.8	86°	-12.34°	15.04°	2.7°	88.7°
O1	5.2	76°	-12.34°	13.94°	1.6°	77.6°
P1	5.8	83°	-12.34°	14.96°	2.6°	85.6°
S1	1.5	275°	-12.34°	15°	2.7°	277.7°
Livello medio del mare Zo=26 cm

La componente k° è stata trasformata in g° essendo la longitudine di Venezia 12.3375° e l'ora fuso=+1.
Laddove venga fornito direttamente il valore g° (come ad.es. nella Tavole di Marea dell'Istituto Idrografico Italiano) è ovvio che la conversione non deve essere effettuata.
Consideriamo la previsione per le ore 15.00 del 10 Marzo 2014 e quindi t=1647 ore.
Dalla tabella interattiva di cui sopra abbiamo ricavato i fattori nodali per il 1.o Gennaio 2014, e quindi si ha

Componente	f	(Vo+u)	om*t	g°	fase (Vo+u)+om*t-g°
M2	1.034	10.4°	216.8°	312.3°	274.9°
S2	1.0	0°	90.0°	323.3°	126.7°
N2	1.034	27.5°	40.2°	310.8°	116.7°
K2	0.769	209°	225.3°	316.4°	117.9°
K1	0.896	14.9°	292.6°	88.7°	218.8°
O1	0.829	353.2°	284.2°	77.6°	199.8°
P1	1.0	349.4°	157.4°	85.6°	61.2°
S1	1.0	180°	225.0°	277.7°	127.3°
Livello medio del mare Zo=26 cm

da cui si ricava l'altezza di ogni componente per l'istante considerato e quindi l'altezza della marea sul livello del mare (l'angolo di fase risultante è stato ridotto, ove necessario, all'angolo giro)

Componente	calcolo f*H*cos(fase)	altezza
M2	1.034*24.8*cos(274.9)	-2.2
S2	1.0*14.5*cos(126.7)	-8.7
N2	1.034*4.1*cos(116.7)	-1.9
K2	0.769*4.3*cos(117.9)	-1.5
K1	0.895*17.8*cos(218.8)	-12.4
O1	0.829*5.2*cos(199.8)	-4.1
P1	1.0*5.8*cos(61.2)	2.8
S1	1.0*1.5*cos(127.3)	-0.9
Somma delle altezze		-24.5
Livello del mare		26.0
Altezza della marea		1.5

Ulteriore precisazione
Il metodo di calcolo esposto è quello tradizionale e, come già detto, si basa sulla determinazione dei valori nodali per la data convenzionale del primo gennaio dell'anno, considerati costanti per tutta la durata di tale anno, e l'aggiunta della variazione di fase dal 1.o gennaio fino all'istante considerato. Questo metodo è dovuto alla difficoltà di calcolare gli elementi nodali per un ben preciso istante quando ancora non esistevano i computer e la necessità, dunque, di utilizzare tabelle precalcolate.
Oggi, sebbene il calcolo dei fattori nodali sia relativamente complesso, grazie all'informatica è possibile calcolare f e Vo+u per un qualsiasi istante, sia con i normali linguaggi di programmazione sia utilizzando un foglio elettronico.
In questo caso il calcolo ovviamente diventa più preciso e, una volta determinati f e Vo+u non occorre calcolare la variazione di fase dal 1.o di Gennaio all'istante voluto.

Ripetiamo il calcolo già effettuato più sopra per Venezia anche con questa modalità e forniamo un altro calcolatore di fattori nodali, non più per la data convenzionale del 1.o Gennaio/1.o Luglio ma proprio per un istante qualsiasi ed impostato per l'occasione per la nostra data di riferimento, anche se ovviamente modificabile a piacere

Calcolatore Fattori Nodali istantanei
Giorno: Mese: Anno: Ora: Min: Sec:
Componente	f	(Vo+u)°
M2
S2
N2
K2
K1
O1
P1
S1
M4
MS4

Il fattore "f" e la parte variabile "u" di (Vo+u) sono calcolati per l'istante considerato.

In questo caso il calcolo della fase finale diventa

Componente	f	(Vo+u)	g°	fase (Vo+u)-g°
M2	1.033	227.4°	312.3°	275.1°
S2	1.0	90.0°	323.3°	126.7°
N2	1.033	68.0°	310.8°	117.2°
K2	0.781	76.0	316.4°	119.6°
K1	0.903	308.4°	88.7°	219.7°
O1	0.841	276.2°	77.6°	198.6°
P1	1.0	146.8°	85.6°	61.2°
S1	1.0	45.0°	277.7°	127.3°
Livello medio del mare Zo=26 cm

e quindi l'altezza della marea sul livello del mare

Componente	calcolo f*H*cos(fase)	altezza
M2	1.033*24.8*cos(275.1)	2.3
S2	1.0*14.5*cos(126.7)	-8.7
N2	1.033*4.1*cos(117.2)	-1.9
K2	0.781*4.3*cos(119.6)	-1.7
K1	0.903*17.8*cos(219.7)	-12.4
O1	0.841*5.2*cos(198.6)	-4.1
P1	1.0*5.8*cos(61.2)	2.8
S1	1.0*1.5*cos(127.3)	-0.9
Somma delle altezze		-24.6
Livello del mare		26.0
Altezza della marea		1.4

Come si nota non c'è una grande differenza rispetto al metodo tradizionale, anche se in alcuni casi le differenze possono risultare leggermente superiori.