LE COORDINATE ASTRONOMICHE ALTAZIMUTALI
Per rappresentare ed indicare la posizione di un qualunque astro sulla S.C. si
utilizzano dei sistemi di coordinate, esattamente come sulla Terra si utilizza la
Latitudine e la Longitudine per indicare la posizione geografica di un luogo.
In Astronomia si impiegano correntemente diversi sistemi, a seconda delle
circostanze. In questa sede elencheremo soltanto i più semplici ed intuitivi.
Il modo più naturale per indicare la posizione di un astro nel cielo è quello di
fornire la direzione verso la quale esso è osservabile e la sua elevazione al di
sopra dell’orizzonte. Queste due indicazioni, date in forma numerica diventano una
coppia di coordinate che prendono nome rispettivamente di azimuth e altezza. Il
piano di riferimento di queste due coordinate è l’orizzonte dell’osservatore; per
altezza si intende l’angolo verticale compreso tra l’orizzonte e la visuale
dell’astro e si indica con la lettera h; ha un valore minimo di 0° (astro sull’orizzonte, che sorge o che
tramonta) e massimo di 90° (astro allo Zenith, sulla verticale della nostra testa).
L’altezza può essere angolarmente estesa anche sotto l’orizzonte: in questo caso
l’osservatore non può misurarla non potendo osservare l’astro e l’altezza si
esprime con valori negativi.
Il cerchio lungo il quale si misura l'altezza prende il nome di cerchio verticale e per altezza si intende anche il corrispondente arco compreso tra orizzonte ed astro. Il cerchio verticale passa per lo Zenith ed è sempre perpendicolare all'orizzonte.
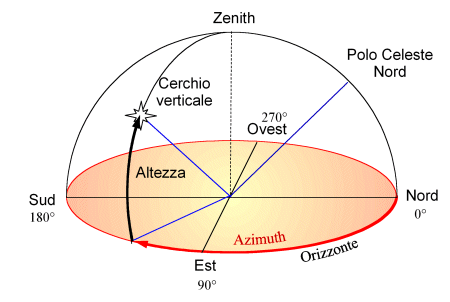
Le coordinate locali altazimutali (o orizzontali)
Anche l’azimuth, indicato con la lettera a o az, si esprime sotto forma di angolo e viene misurato sul piano
dell’orizzonte. Come direzione di
riferimento in genere (in particolare i marinai) si assume la direzione del Nord
geografico (gli astronomi preferiscono però utilizzare la direzione del Sud) e
l’angolo viene contato in senso orario da 0° a 360°. In questo modo i punti cardinali
Nord, Est, Sud ed Ovest hanno rispettivamente azimuth 0°, 90°, 180°, 270°.
L’altezza si misura con uno strumento che i marinai chiamano sestante; l’azimuth si
misura con la bussola.
Questo sistema di coordinate prende il nome di altazimutali ed è legato
esclusivamente alla posizione dell’osservatore. Sono cioè coordinate locali e non
universali. Questo significa che due osservatori posti in luoghi diversi, vedranno lo
stesso astro nello stesso istante con valori di azimuth e altezza diversi.
Non solo, poiché la S.C. è dotata di moto apparente e quindi gli astri si muovono
rispetto all’orizzonte, le coordinate altazimutali di tutti gli astri sono
continuamente mutevoli, per cui, quando si vogliono indicare occorre sempre
specificare l’ora di osservazione.
Una applicazione interessante. Descrivendo la S.C., nella prima parte, abbiamo
accennato che l’Asse del Mondo forma con l’orizzonte un angolo pari alla
Latitudine. Se potessimo direttamente osservare il Polo Celeste Nord e misurarne
l’altezza con il sestante otterremmo direttamente e semplicemente la Latitudine
del luogo. I marinai, ancora oggi, sebbene sempre più raramente, è così che misurano
la Latitudine in mezzo al mare: misurando l’altezza della Stella Polare.Questo
metodo estremamente semplice ha consentito agli astronomi e ai geografi sin dalla
antichità di misurare la latitudine di un luogo. La determinazione della longitudine
è invece stato un grosso problema che solo un paio di secoli addietro ha trovato
definitiva soluzione.
L’altezza e l’azimuth essendo legate alla visibilità da parte dell’osservatore sono
le uniche direttamente misurabili e sono quelle mediante le quali vediamo, viviamo e
descriviamo il cielo; sono, come dire, le coordinate finali dell’utente.
Esistono altri sistemi di riferimento meno immediati ed intuitivi ma più universali e più
adatti ai calcoli astronomici.
Nell'ambito dei calcoli trigonometrici che occorre affrontare per la risoluzione dei problemi di AStronomia Nautica, talvolta, anzi direi spesso, in luogo dell'azimuth si usa l'Angolo Azimutale. Il vantaggio è che quest'ultimo ha una valore sempre inferiore a 180°, proprietà che, vedremo è particolarmente utile nello studio dei triangoli sferici.
L'Angolo Azimutale si conta, sempre sull'orizzonte, ma a partire dal cardine Nord, nell'emisfero Nord, dal cardine Sud, nell'emisfero Sud, sino al verticale dell'astro.
Per eliminare eventuali ambiguità al valore numerico si premette sempre il segno della Latitudine (N o S) e si fa seguire quello dell'emisfero occidentale (W) od orientale (E) in cui è posto l'astro.
Ad esempio, In Latitudine Nord un astro che ha azimuth 60° ha angolo azimutale N60°E (in questo unico caso i due valori numerici coincidono.
In Latitudine Sud l'angolo azimutale sarebbe S120°E.
Altro esempio: in Latitudine Nord un astro con Azimuth 320° ha un angolo azimutale N40°W, e così via.
La seguente tabella illustra le relazioni tra azimuth e l'angolo azimutale (che si indica con la lettera Z maiuscola sormontata dall'accento circonflesso.
| Latitudine |
|
Azimuth |
Ang.azimutale |
|
Ang.azimutale |
Azimuth |
| Nord |
|
0°-180° |
N (azimuth) E |
|
N ang.az. E |
ang.az. |
| Nord |
|
180°-360° |
N (360-azimuth) W |
|
N ang.az. W |
360-ang.az. |
| Sud |
|
0°-180° |
S (180-azimuth) E |
|
S ang.az. E |
180-ang.az. |
| Sud |
|
180°-360° |
S (azimuth-180) W |
|
S ang.az W |
ang.az+180 |
LE COORDINATE ASTRONOMICHE ORARIE
Abbiamo visto che il piano di riferimento delle coordinate altazimutali è
l’orizzonte; bene, se prendiamo come riferimento il piano dell’Equatore celeste ed
ad esso applichiamo per analogia i concetti, ovviamente modificati, di azimuth ed
altezza otteniamo un sistema di coordinate che prende il nome di sistema locale orario.
Locale, perchè in parte è ancora legato alla posizione dell’osservatore (sebbene
già con una certa proiezione all’universalità) e orario in quanto almeno una delle
coordinate è funzione diretta del tempo ed il sistema è legato alla traiettoria
diurna apparente dell’astro sulla S.C.
Un astro per effetto del suo moto (apparente) diurno lascia sulla S.C. una traccia
circolare e parallela all’Equatore Celeste; tale traccia prende nome di parallelo
di declinazione e la sua posizione è esprimibile con la distanza angolare che lo separa
dall’Equatore stesso.
Tale angolo è la declinazione. Se torniamo mentalmente alle coordinate
altazimutali essa è, rispetto all’Equatore, ciò che l’altezza è rispetto
all’orizzonte.
Anche la declinazione ha valore massimo 90° (Polo Celeste) e minimo 0° (astro
sull’Equatore); anch’essa si misura con valori positivi (convenzionalmente per gli
astri che appartengono all’emisfero Nord) e negativi (astri dell’emisfero Sud).
Esempio: la stella Polare, che coincide con il Polo Celeste Nord ha declinazione
+90° (oppure 90° Nord).
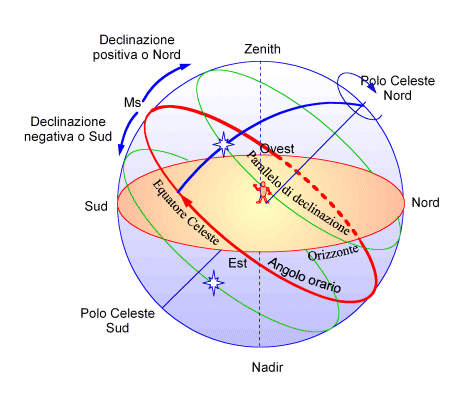
Fig. 4 - Le coordinate locali orarie
Essendo la declinazione di un astro riferita all’Equatore non è legata alla posizione
dell’osservatore; non è quindi una coordinata locale bensì universale ed
invariabile. Essa vale quindi per tutti gli osservatori, qualunque sia la loro
latitudine e qualunque sia l’istante dell’osservazione. Un astro, per il solo effetto
del moto diurno, non muterà mai il suo valore di declinazione.
L’altra coordinata che fa coppia con la declinazione è, sempre per tornare alla
nostra analogia, quello che l’azimuth è per l’orizzonte e prende nome di angolo
orario o tempo dell’astro (Fig. 4). Il tempo è l’arco di Equatore, misurato in gradi ed in
senso orario a partire dal punto di incontro tra meridiano celeste superiore ed Equatore (punto che prende il nome di mezzocielo superiore e si ndica con Ms), da 0° a 360° (gli astronomi
preferiscono misurarlo in ore da 0 a 24). Poichè si parla di meridiano, e quindi si fa
riferimento alla posizione dell’osservatore, l’angolo orario è una coordinata
locale, che vale solo per tale osservatore e per un dato istante. L’angolo orario
cambia continuamente ma soprattutto uniformemente (cosa, quest’ultima, che non
fanno ad es. nè l’azimuth nè l’altezza) in funzione del tempo che passa e al ritmo di
15° in un ora, 1° ogni 4 minuti, 15’ al minuto ecc.
Con esso si può misurare il tempo o la sua variazione (ed è per questo che ne ha assunto
anche il nome). Un astro che è al meridiano superiore ha angolo orario pari a 0° e
poichè rispetto agli istanti del sorgere e del tramonto ha percorso metà del suo
arco diurno è al suo mezzogiorno; in tale istante la sua altezza è la massima
raggiungibile. Se il suo angolo orario è 180° è al meridiano inferiore e quindi alla
sua mezzanotte.
Un astro che ha declinazione zero si muove lungo l’Equatore: sorge esattamente
sul punto cardinale Est (azimuth =90°) e tramonta sul punto Ovest (az.=270°);
sorge 90° (6 ore) prima di passare in meridiano e tramonta 90° dopo: il suo arco
diurno dura 12 ore esatte, tanto quanto l’arco notturno.
Analogamente a quanto visto per l'azimuth, anche per l'angolo orario nei calcoli si usa spesso il suo valore ridotto a meno di 180°. In questo caso di parla di Angolo al Polo. Esso si misura sempre dal meridiano superiore (qualunque sia il segno della Latitudine), verso Est o verso Ovest a seconda della posizione dell'astro.
La conversione in questo caso è più semplice; se l'angolo orario è minore di 180°, l'astro è nell'emisfero occidentale e l'angolo al polo è numericamente uguale all'angolo orario, ma seguito dal suffisso W.
Se l'angolo orario è maggiore di 180° l'angolo al polo è pari a (360°-angolo orario) ed è seguito dal suffisso E.
L'angolo al polo si indica con la lettera P maiuscola sormontata dall'accento circonflesso.
La tabella riporta le relazioni tra i due angoli.
| Angolo orario |
Angolo al polo |
| 0°-180° |
(ang.orario) W |
| 180°-360° |
(360-ang.orario) E |
|

