Home page

IL PUNTO NAVE ASTRONOMICO Corso online di Astronomia Nautica precedente               seguente

TRASFORMAZIONE DI COORDINATE Nota. Si dà per scontato che l'utente sia in grado di effettuare le operazioni elementari sui gradi in formato sessagesimale, abbia una minima conoscenza delle funzioni trigonometriche, e sappia utilizzare una normale calcolatrice scientifica. Va bene anche quella disponibile su Windows. Le funzioni arcoseno e arcocoseno sono inverse, rispettivamente, al calcolo del seno e del coseno. Nella maggior parte delle calcolatrici le funzioni arcoseno e arcocoseno si attivano premendo i tasti INV sin e INV cos, oppure 2nd sin e 2nd cos, fornendo così il relativo angolo espresso in gradi decimali. Attenzione però; questa regola non vale per tutte le calcolatrici che possono adottare anche soluzioni diverse. Documentatevi su come la vostra calcolatrice effettivamente fornisce le funzioni trigonometriche inverse. Per la determinazione del Punto Nave Astronomico occorre risolvere il triangolo di posizione determinando l'altezza e l'azimuth per ogni astro osservato, partendo dalle sue coordinate equatoriali, che sono note e riportate nelle Effemeridi. Occore cioè eseguire una trasformazione di coordinate. Prendiamo in considerazione il triangolo di posizione, i cui elementi ci sono noti e determiniamone il lato z (distanza zenitale) essendo noti la Latitudine, l'angolo al polo e la declinazione dell'astro. Determinare la distanza zenitale significa determinare l'altezza dell'astro, che è l'incognita che ci interessa. 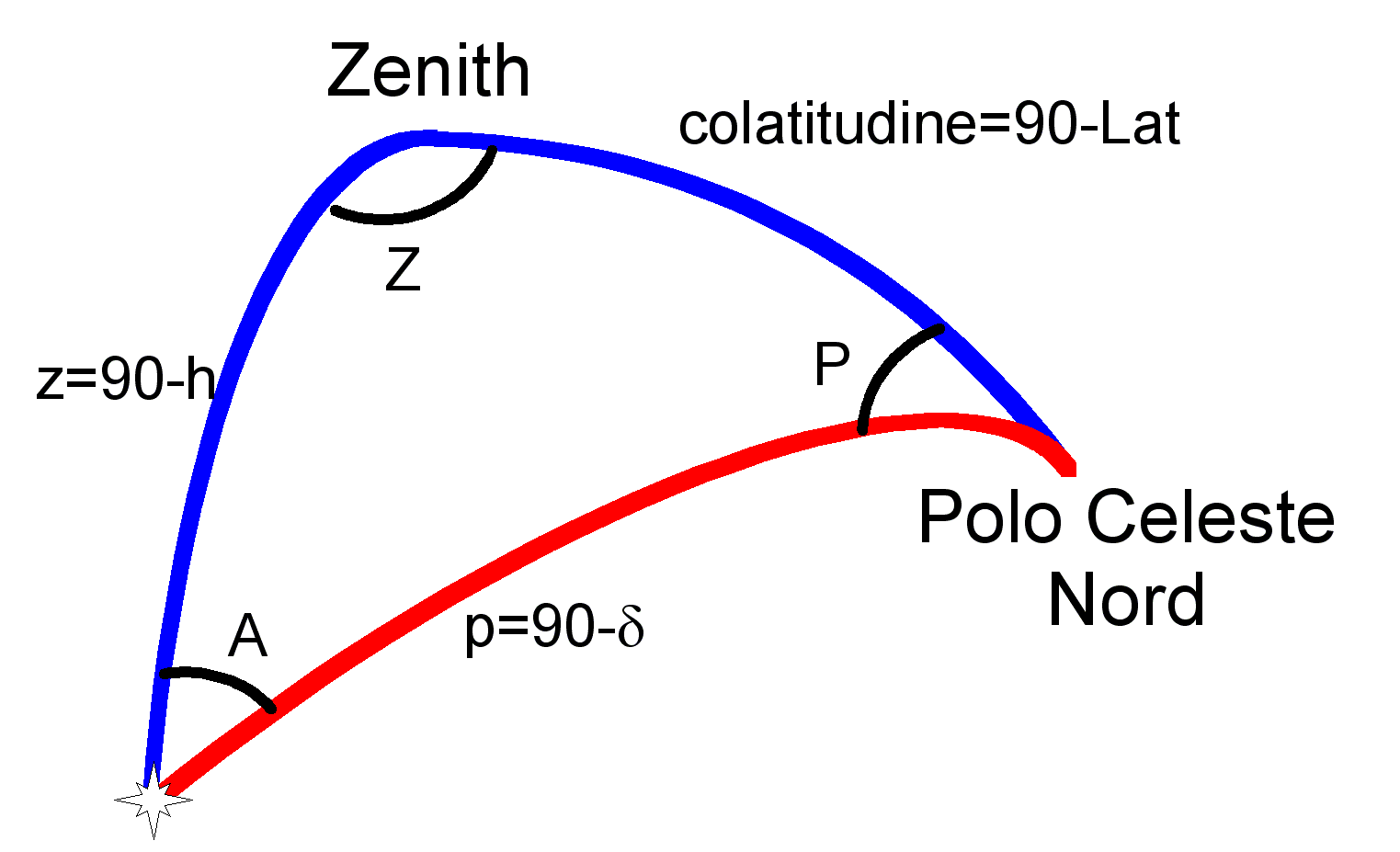CALCOLO DELL'ALTEZZA Applichiamo la formula di Eulero diretta al lato z: cos(z) = cos(c) cos(p) + sen(c) sen(p) cos(P) ed essendo z=90-h, p=90-decl e c=90-Lat si ha cos(90-h) = cos(90-Lat) cos(90-decl) + sen(90-Lat) sen(90-decl) cos(P) e poichè i coseni degli angoli complementari si possono sostituire con i seni e viceversa si ottiene la formula finale sen(h) = sen(Lat) sen(decl) + cos(Lat) cos(decl) cos(P) che permette di calcolare l'altezza in gradi, effettuando l'arcoseno del risultato. h° = arcoseno(sen(Lat) sen(decl) + cos(Lat) cos(decl) cos(P)) Il risultato è sempre compreso tra -90 e +90°. Un valore negativo indica che l'astro è al di sotto dell'orizzonte. Segue un esempio Siano Latitudine 40°N, Angolo Orario 290°, Declinazione 30°N L'Angolo Orario va trasformato nel corrispondente Angolo al Polo 70°W La formula diventa: h° = arcoseno(sen(40) sen(30) + cos(40) cos(30) cos(70)) con la calcolatrice scientifica si ottiene (usando almeno cinque decimali) h° = arcoseno(0.64279 x 0.5 + 0.76604 x 0.86602 x 0.34202) che sviluppata fornisce h° = arcoseno(0.32139 + 0.22690) = arcoseno(0.54829) attivando la funzione inversa del seno (arcoseno) sulla calcolatrice si ottiene l'altezza in gradi decimali trasformati in gradi e primi h° = 33°.25 = 33°15' poichè il valore è positivo l'astro è sopra l'orizzonte e dunque visibile. Si osserva che l'Angolo al Polo pur essendo di segno Ovest (W) va inserito nella formula con il segno algebrico positivo. CALCOLO DELL'AZIMUTH Applicando la formula di Eulero in modalità inversa all'angolo Z, ed omettendo i passaggi intermedi si può calcolare l'altra incognita che ci interessa, l'azimuth, non direttamente ma attraverso l'angolo azimutale Z, ed utilizzando l'altezza calcolata con il passo precedente. cos(Z) = (sen(decl) - sen(Lat) sen(h)) / (cos(Lat) cos(h)) Come al solito l'angolo azimutale in gradi si ottiene eseguendo l'arcocoseno del risultato. Z° = arcocoseno((sen(decl) - sen(Lat) sen(h)) / (cos(Lat) cos(h))) Segue un esempio Siano Latitudine 40°N, Angolo Orario 290°, Declinazione 30°N L'Angolo Orario va trasformato nel corrispondente Angolo al Polo 70°W (per tenere conto del suffisso) La formula diventa: Z° = arcocoseno(sen(30)- sen(40) sen(33.25))/(cos(40) cos(33.25)) con la calcolatrice scientifica si ottiene (usando almeno cinque decimali) Z° = arcocoseno(0.5-0.64279 x 0.54829)/(0.76604 x 0.83629) Z° = arcocoseno(0.5-0.35243)/0.64063 = 0.14757/0.64063 = 0.23035 attivando la funzione inversa del coseno (arcocoseno) sulla calcolatrice si ottiene l'Angolo Azimutale in gradi decimali (non c'è bisogno di trasformarlo in gradi e primi) Poichè l'Angolo al Polo ha suffiso W, l'Angolo azimutale si conta da N verso W. Ad esso corrisponde un azimuth pari a 283°.3 Z° = N 76°.7 W ----> azimuth = 283°.3 Il risultato è un angolo sempre compreso tra 0° e 180°. In entrambe le formule la Latitudine e la Declinazione dell'astro vanno inserite con il loro segno algebrico (cioè positivo se Nord e negativo se Sud). L'angolo al Polo va sempre inserito con valore positivo. Con queste regole si ottiene l'angolo azimutale con prefisso sempre N e suffisso W o E a seconda che l'angolo orario sia rispettivamente minore (astro ad occidente) o maggiore (astro ad oriente) di 180°; cioè che l'Angolo al Polo sia di segno W o E. In breve l'angolo azimutale ha sempre lo stesso suffisso dell'Angolo al Polo. Dall'angolo azimutale si passa all'azimuth secondo le regole già viste. Naturalmente si può effettuare anche la trasformazione inversa, cioè da altezza ed azimuth ad angolo al polo e declinazione; tale conversione si applica in casi specifici che però in questa sede non saranno affrontati. In queste formule tutti i dati sono noti, tranne l'angolo al Polo che non sappiamo ancora calcolare. Sarà argomento delle prossime lezioni. Una curiosità. Come fa la Latitudine ad essere nota se è proprio una delle coordinate del Punto Nave che vogliamo determinare? Come abbiamo già accennato in realtà non si determinano direttamente Latitudine e Longitudine ma la loro distanza rispetto ad un punto approssimato che serve di appoggio al calcolo. Il Punto Nave si determina a partire da un Punto Stimato, ed è la Latitudine di quest'ultimo che viene usata nei calcoli. Sotto è riportata un'applicazione Javascript che inserendo le coordinate Equatoriali le converte in coordinate altazimutali. Fate qualche prova.

Trasformazione di coordinate

da coordinate Equatoriali orarie Latitudine: Declinazione: Angolo al Polo: E W

a coordinate altazimutali Altezza: Angolo azimutale: Azimuth:

Nota: Qualche esperto nel constatare che la formula per il calcolo dell'azimuth richiede necessariamente il precalcolo dell'altezza, storcerà probabilmente il naso.
Esiste infatti un'altra formula per il calcolo dell'azimuth che è indipendente dal calcolo dell'altezza (e quindi da suoi eventuali errori) e si basa sugli stessi elementi già usati per il calcolo dell'altezza. Il suo uso però, per i non esperti, è un po' complicato. Abbiamo preferito fornire la procedura di cui sopra che è più semplice, considerato che, comunque, l'altezza deve essere calcolata.

precedente        Inizio pagina       seguente