I QUADERNI DELL'ALMANACCO
L'ASTROLABIO
di Franco Martinelli
(4)
LA PROGETTAZIONE DELLA RETE
LE STELLE A differenza della lamina che è funzione della latitudine dell'osservatore, il disegno della rete è identico per tutti gli astrolabi, rappresentando la posizione delle stelle cosiddette "fisse" ed il percorso annuale del Sole rispetto ad esse, cioè l'eclittica.Osservando diversi modelli di astrolabio si noterà, invece, che le reti possono differire anche notevolmente l'una dall'altra. Nel descrivere, nella seconda parte di questa monografia, la struttura dell'astrolabio ed in particolare della rete, abbiamo già spiegato che tali differenze sono dovute alla quantità di stelle rappresentate e quali si sia preferito rappresentare. Poichè la rete necessariamente è lavorata traforo per consentire la visione e la lettura della lamina sottostante, le stelle vengono indicate da "punte" variamente lavorate a forma di fiammella, o a punta di lancia o freccia, sostenute da una telaio di archi o segmenti che attraversano il disco. La forma del telaio e la posizione dei bracci che lo costituiscono è legata alla posizione delle punte. Questo è uno dei motivi della estrema variabilità dell'aspetto delle reti.
Occorre però tenere in considerazione anche un altro elemento: il fenomeno della precessione degli Equinozi che fa si che le stelle fisse, proprio fisse non lo siano. Senza voler entrare nei dettagli ricordiamo brevemente che per tale fenomeno tutte le stelle, in blocco, subiscono uno slittamento parallelo al piano dell'Eclittica. Cambia la loro longitudine celeste e resta pressochè invariata la latitudine. In questo slittamento la posizione reciproca delle stelle rimane immutata. Il fenomeno è lentissimo, inapprezzabile nell'arco di tempo della vita di un uomo, ma al passare dei secoli gli effetti cominciano a farsi sentire.
Tanto per quantificare il fenomeno, in 2000 anni le stelle si spostano di circa 30°.
Questo comporta sostanzialmente due cose. Il percorso annuo del Sole sullo sfondo delle stelle rimane immutato ma cambiano i tempi in cui esso incontra le diverse costellazioni. Seconda conseguenza è che le stelle visibili ad una data latitudine cambiano. Grazie a questo slittamento, nei secoli, stelle che prima erano visibili ad un certo punto scompaiono ed altre, che erano invisibili, si mostrano al di sopra dell'orizzonte.
In questa maniera è evidente che una rete disegnata nel medioevo non può essere utilizzata ai giorni nostri e comunque che ogni rete è irrimediabilmente "datata"; la posizione delle stelle deve essere calcolata per il periodo in cui si vuole utilizzare lo strumento e, tenendo conto della sua comunque limitata precisione, ha una durata non superiore ad un centinaio di anni.
Ciò premesso passiamo alla costruzione della rete utilizzando un disco dello stessso diametro della lamina e riportandovi sopra la posizione di un certo numero di stelle, opportunamente selezionate.
Si dovrà successivamente lavorare a traforo il disco in modo da mettere in evidenza le stelle rispetto alle linee tracciate sulla sottostante lamina.
Non dimentichiamo che il disco della rete deve essere sovrapposto a quello della lamina.
La posizione delle stelle che proponiamo è stata calcolata per l'anno 2000. Vuol dire che il nostro strumento potrà essere usato per calcoli compresi tra il 1950 ed il 2050, decennio più, decennio meno.
Essendo l'astrolabio una proiezione sul piano dell'Equatore celeste, la posizione delle stelle va fornita in coordinate equatoriali, e cioè ascensione retta e declinazione.
La declinazione è la distanza angolare rispetto all'Equatore e che noi dovremo trasformate in distanza lineare; l'ascensione retta è l'angolo, misurato in senso antiorario lungo l'Equatore da un punto fisso convenzionale di riferimento e la stella considerata. Il riferimento prende nome di "Punto Gamma" e corrisponde al punto in cui passa il Sole nell'istante dell'Equinozio di primavera, quando attraversando l'Equatore transita dall'Emisfero celeste Sud a quello Nord.
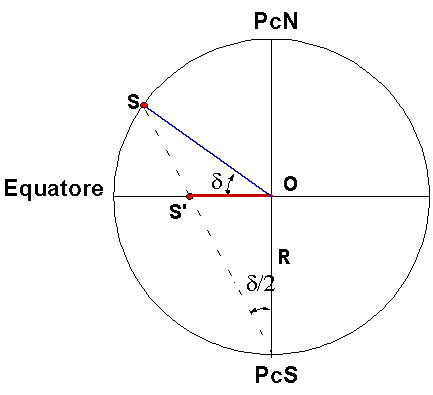
Vista laterale della sfera celesteDalla figura si ricava il valore della distanza lineare OS' in funzione della declinazione delta dell'astro S.
Osservando dall'alto la sfera celeste nella figura sottostante, cioè sul prolungamento del Polo Celeste Nord, si comprende anche il ruolo dell'ascensione retta, indicata con la lettera alfa, nel posizionamento della generica stella S. L'angolo alfa rimane invariato durante la proiezione grazie alla proprietà di conservazione degli angoli della proiezione stereografica.OS' = R tan((90-delta)/2)

Vista sulla proiezione dell'Equatore
Posizionare le stelle sarà dunque semplice. Scelte le più opportune, se ne calcolerà la distanza dal centro in funzione della declinazione e, scelta arbitrariamente la direzione del Punto Gamma, basta riportare tale distanza con un angolo pari all'ascensione retta.
Qui di seguito forniamo la tabella di ventiquattro stelle, con i valori già pronti per il trasferimento sul disco.Attenzione! Ascensione e declinazione, per comodità di calcolo, sono riportate in formato decimale e non sessagesimale.Nome stella Asc.Retta Declinazione Distanza X Y 1 ALPHERATZ 2.10 29.10 2.50 2.50 0.09 2 DENEB KAITOS 10.90 -17.98 5.85 5.74 1.11 3 MIRFAK 51.08 49.87 1.55 0.98 1.21 4 ALDEBARAN 68.98 16.52 3.17 1.14 2.96 5 RIGEL 78.63 -8.20 4.91 0.97 4.81 6 CAPELLA 79.18 46.00 1.72 0.32 1.69 7 BELLATRIX 81.28 6.35 3.80 0.58 3.76 8 ALNILAM 84.05 -1.20 4.34 0.45 4.32 9 MIRZAM 95.68 -17.95 5.84 -0.58 5.82 10 ALHENA 99.43 16.40 3.18 -0.52 3.14 11 SIRIO 101.28 -16.72 5.71 -1.12 5.60 12 ADHARA 104.67 -28.97 7.21 -1.83 6.98 13 PROCIONE 114.83 5.22 3.88 -1.63 3.52 14 ALPHARD 141.90 -8.67 4.95 -3.89 3.05 15 GIENAH 183.97 -17.53 5.80 -5.79 -0.40 16 ALIOTH 193.50 55.95 1.30 -1.27 -0.30 17 SPICA 201.30 -11.17 5.17 -4.82 -1.88 18 ARTURO 213.92 19.18 3.02 -2.51 -1.69 19 ANTARES 247.35 -26.43 6.86 -2.64 -6.33 20 RASALAGUE 263.73 12.57 3.41 -0.37 -3.39 21 VEGA 279.23 38.78 2.04 0.33 -2.01 22 ALTAIR 297.68 8.87 3.64 1.69 -3.22 23 DENEB 310.35 45.28 1.75 1.13 -1.33 24 FOMALAUT 344.35 -29.62 7.30 7.03 -1.97
Sono state riportate le posizioni anche in termini di coordinate cartesiane, assumendo come asse positivo delle x la direzione del Punto Gamma e asse delle y la sua perpendicolare passante per il centro del disco.
La distanza e l’angolo possono essere infatti trasformati, per un più semplice posizionamento, in coordinate catesiane x e y mediante le formulex = d*cos(alfa) y = d*sen(alfa)per un più semplice posizionamento.
Posta dunque la direzione del Punto Gamma sulla destra, i valori di x si devono intendere, come nelle normali coordinate cartesiane, positivi a destra del centro del disco e a sinistra se negativi; i valori delle y andranno riportati in alto se positivi e in basso se negativi.
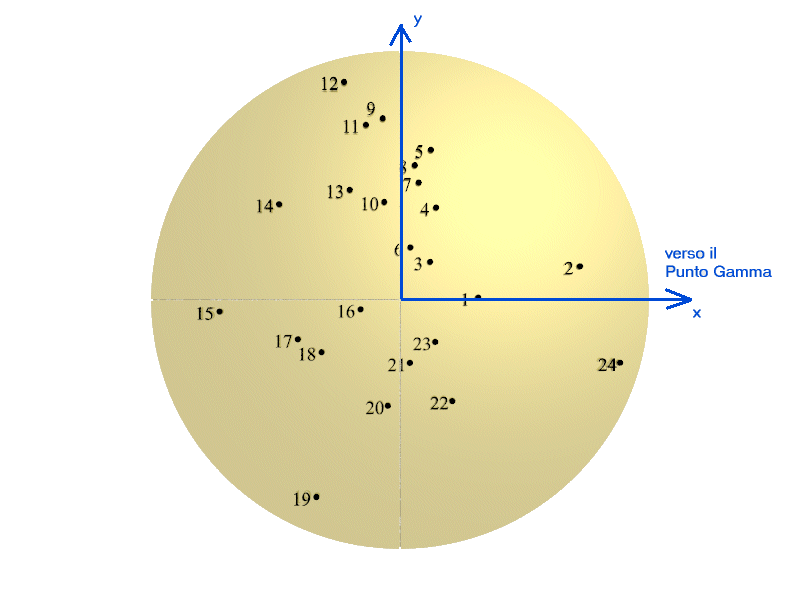
Le stelle di cui sopra risultano così distribuite sul disco che poi sarà quello dal quale si ritaglia la rete:
L'ECLITTICA
L'eclittica viene rappresentata come una circonferenza. Le sue dimensioni sono fisse e, ovviamente, indipendenti dalla latitudine dell'osservatore.
I due punti estremi, al di sopra e al di sotto dell'Equatore sono i Solstizi, i punti cioè in cui il Sole assume la massima distanza dall'Equatore. Le loro distanze rispetto al centro del disco sono: 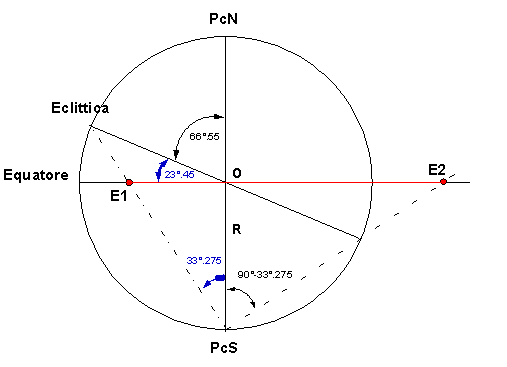
OE1= R tan(33°.275) OE2 = R tan(56°.725)Nel nostro caso specifico,avendo assunto il raggio R della sfera pari a 4.25 si haOE1= 4.25 tan(33°.275) = 2.79 OE2 = R tan(56°.725) = 6.48La posizione di questi due punti individua fli estremi deldiametro della eclittica proiettata sull'Equatore; il centro sarà pertanto equidistante da essi e posto alla distanza(6.48 - 2.79) / 2 = 1.84nella direzione del Soltizio più lontano (E2), e precisamente quello invernale.
Il raggio dell'eclittica proiettata sarà:(6.48 + 2.79) / 2 = 4.63La direzione dei Solstizi è perpendicolare a quella degli Equinozi e pertanto, fissata inizialmente la direzione del Punto Gamma (che corrisponde all'Equinozio primaverile), sarà semplice tracciare la proiezione dell'Eclittica sulla rete.I punti notevoli che risultano in figura sono:
C Centro dell'Eclittica EP Equinozo Primaverile SE Solstizo Estivo EA Equinozio Autunnale SI Solstizio Invernaleche il Sole, nel suo moto annuo percorre i senso antiorario.
Gli astronomi dell'antichità, per fissare la posizione del Sole, dividevano l'Eclittica in 12 zone ampie 30°, ciascuna associata ad un segno zodiacale. Per indicare la posizione del Sole ci si riferiva al segno e al numero di gradi nel suo interno; così, ad es. si usava dire che il Sole era nell'8.vo grado del Leone, nel 23.mo grado dell'Ariete e così via.
Il punto di partenza era il Punto Gamma, chiamato anche Punto Vernale (vernale sta per primaverile), Primo Punto o Testa dell'Ariete.
Ancora oggi contiamo le longitudini eclittiche a partire dall'Equinozio Primaverile ma con continuità da 0° a 360° senza più fare riferimento ai segni.
Così il Punto Gamma ha longitudine zero gradi, Il Solstizio Estivo 90°, l'Equinozio d'Autunno 180° e il Solstizio Invernale 270°.
Trattandosi di una proiezione sul piano equatoriale non è purtroppo possibile suddividere direttamente l'eclittica nei settori zodiacali. E' pur vero che essendo l'astrolabio una proiezione stereografica, e quindi mantenendosi inalterati gli angoli, si potrebbero riportare le longitudini dal centro dell'Eclittica con un normale goniometro ma i meridiani assumerebbero una forma curvilinea non facile da riprodurre.
E' possibile però trasformare la longitudine eclittica in ascensione retta che per sua natura si misura proprio sul piano dell'Equatore.
Nel disegno a fianco (che rappresenta solo il disco dell'Eclittica e non tutta la rete) in rosso sono tracciati i meridiani per l'inizio di gni segno zodiacale. Essi si dipartono dal polo eclitticale e, in quanto cerchi sulla sfera, sono riprodotti con archi di circonferenza sulla proiezione stereografica.
In nero sono invece disegnate le corrispodenti ascensioni rette che originano dal centro dell'astrolabio (Polo Celeste Nord) e pur essendo cerchi sulla sfera sono riprodotti sotto forma di segmenti in quanto i piani che li contengono passano tutti per il punto di vista (Polo Celeste Sud). Tracciare quest'ultimi, e individuare sull'Eclittica le divisioni tra i segni, è ovvamente più semplice.
Mettiamo in evidenza che il centro geometrico C della proiezione dell'Eclittica non coincide con la proiezione del Polo Eclitticale (E), rispetto al quale si misurano le longitudini; il centro geomerico O dell'astrolabio coincide invece con la proiezione del Polo Celeste Nord, rispetto al quale si misurano le ascensioni rette.
La formula che mette in relazione ascensione retta, longitudine ed obliquità eclittica è la segente:ove valore dell'obliquità è considerato pari a 23°26'.tan(ascens.) = tan(long.) * cos(obliquità)
Qui di seguito forniamo i valori di ascensione retta per ogni 5° di longitudine, in base ai quali sarà possibile contrassegnare l'Eclittica con la posizione che mediamente assume il Sole ogni 5 giorni. Per il nostro scopo è più che sufficiente ma chi vuole una maggiore risoluzione può calcolarsi l'eclittica ogni singolo grado e cioè praticamente giorno per giorno.Una eclittica così suddivisa si presenta come nella figura sottostante. Abbiamo tagliato la parte centrale e quella esterna lasciando solo una sottile corona circolare diLong. Asc. Long. Asc. Long. Asc. Ariete 5 4,6 50 47,6 95 95,4 10 9,2 55 52,6 100 100,9 15 13,8 Gemelli 60 57,8 105 106,3 20 18,5 65 63,1 110 111,6 25 23,2 70 68,4 115 116,9 Toro 30 27,9 75 73,7 Leone 120 122,2 35 32,7 80 79,1 125 127,4 40 37,6 85 84,6 130 132,4 45 42,5 Cancro 90 90,0 135 137,5 Long. Asc. Long. Asc. Long. Asc. 140 142,4 185 184,6 230 227,6 145 147,3 190 189,2 235 232,6 Vergine 150 152,1 195 193,8 Sagitt. 240 237,8 155 156,8 200 198,5 245 243,1 160 161,5 205 203,2 250 248,4 165 166,2 Scorp. 210 207,9 255 253,7 170 170,8 215 212,7 260 259,1 175 175,4 220 217,6 265 264,6 Bilan. 180 180,0 225 222,5 Capric. 270 270,0 Long. Asc. Long. Asc. 275 275,4 320 322,4 280 280,9 325 327,3 285 286,3 Pesci 330 332,1 290 291,6 335 336,8 295 296,9 340 341,5 Acquar. 300 302,2 345 346,2 305 307,4 350 350,8 310 312,4 355 355,4 315 317,5 Ariete 360 360,0dimensioni sufficienti a contenere le graduazioni e consentire la visione delle stelle al suo interno.
Sottolineiamo ancora una volta che tali divisioni corrispondono alle longitudini celesti, pur avendole individuate tramite le corrispondenti ascensioni rette.
Si potrebbe anche suddividere l'eclittica in base al calendario, riportando su di essa, in luogo delle longitudini, i mesi, le decadi, le cinquine, i singoli giorni. In questa maniera sarebbe senz'altro più semplice e comodo individuare sull'astrolabio la posizione del Sole.
Una suddivisione del genere però è tutt'altro che semplice e lineare a causa della velocità variabile del Sole lungo l'Eclittica e dell'eccentricità dell'orbita terrestre; i mesi, ad anche i singoli giorni non potrebbero essere suddivisi in spazi uniformi e per ognuno di essi occorrerebbe calcolarne la giusta ampiezza.
D'altra parte occorre comunque poter associare alla data di calendario la longitudine del Sole, e viceversa, per poter operare sull'astrolabio. Nelle puntate precedenti abbiamo già spiegato come questo problema di conversione venisse risolto, incidendo sul retro della madre un equatorium cioè un regolo che consentiva una tale operazione.
Ne riparleremo quando prenderemo in esame la costruzione del dorso.
...IN PRATICA
A questo punto il nostro disco delle rete si dovrebbe presentare così.Se abbiamo correttamente dimensionato la corona circolare del'eclittica, questa cade proprio in mezzo alle stelle prescelte e già disegnate, senza occultarne alcuna.
Il problema è che il disco è solido e una volta sovrapposto alla lamina la nasconde comletamente alla nostra vista. Non è quindi possibile riferire la posizione delle stelle e del Sole all'orizzonte dell'osservatore.
Per far questo occorre ritagliare e portare via il più possibile le parti inutili della rete, attraverso le quali sia possibile osservare i cerchi e le linee della lamina.
Qui entra in gioco la fantasia e l'abilità del costruttore di astrolabi. Si tratta di individuare dei percorsi, sotto forma di sottili segmenti o archi, attraverso le stelle e l'eclittica in modo da tenere tutte queste parti solidamente assieme e garantire il massimo di visibilità della sottostante lamina.
Questa variabilità nella ricerca della struttura portante della rete era improntata criteri anche di eleganza e di simmetria, ed era quello che caratterizzava uno strumento dall'altro, rendendolo bello, affascinante e nel contempo, e misterioso.
Oggigiorno si può evitare di traforare il disco della rete, disegnando il tutto su un foglio di plastica trasparente sottile ma resistente. Ciò consentirebbe anche di aumentare il numero delle stelle, ma sarebbe una soluzione poco elegante e non in linea con la tradizione.
Nei prossimi articoli vedremo come realizzare una rete completa in stile medievale, con relativa semplicità.
Occorrerà un po' di abilità manuale, ma veramente minima minima; anche un bambino sarà in grado di raggiungere discreti risultati.